Emnet for denne artikkelen er beregningen av en polykarbonatbaldakin med egne hender. Vi må lære å beregne hovedparametrene til strukturen knyttet til dens styrke og dimensjoner. Så la oss gå.

Hva regner vi ut
Vi må lære å beregne:
- Tykkelsen på polykarbonatet og stigningen på kassen avhengig av forventet snøbelastning per kvadratmeter.
- Dimensjoner for buedeksel (som når det gjelder geometri kommer ned til å beregne lengden på buen).
For å presisere: vi utforsker måter å beregne buen for kjent radius og vinkel på sektoren, så vel som for tilfellet når vi bare kjenner avstandene mellom ytterpunktene på bueoverflaten.
- Minimum rørseksjon med kjent bøyelast.
I denne rekkefølgen går vi videre.
Dreiebenk og beleggtykkelse
La oss starte med beregningen av snølasten.
Før vi finner ut hvordan vi beregner en baldakin av polykarbonat, vil vi formulere et par forutsetninger som beregningen er basert på.
- De gitte dataene er relevante for materiale av høy kvalitet uten tegn til ødeleggelse av ultrafiolett stråling. Polykarbonat uten UV-filter blir sprø etter 2-3 års drift i lys.

- Vi overser bevisst den begrensede deformasjonsstabiliteten til kassen, og vurderer den som absolutt sterk.
Og nå - et bord som vil hjelpe deg å velge den optimale tykkelsen på polykarbonat og stigningen på kassen.
| Last, kg/m2 | Kassecelledimensjoner med polykarbonattykkelse, mm | |||
| 6 | 8 | 10 | 16 | |
| 100 | 1050 x 790 | 1200 x 900 | 1320 x 920 | 1250 x 950 |
| 900 x 900 | 950 x 950 | 1000x1000 | 1100 x 1100 | |
| 820 x 1030 | 900 x 1100 | 900 x 1150 | 950 x 1200 | |
| 160 | 880 x 660 | 1000 x 750 | 1050 x 750 | 1150 x 900 |
| 760 x 760 | 830 x 830 | 830 x 830 | 970 x 970 | |
| 700 x 860 | 750 x 900 | 750 x 950 | 850 x 1050 | |
| 200 | 800 x 600 | 850 x 650 | 950 x 700 | 1100 x 850 |
| 690 x 690 | 760 x 760 | 780 x 780 | 880 x 880 | |
| 620 x 780 | 650 x 850 | 700 x 850 | 750 x 950 | |
Arch
Beregning etter radius og sektor
Hvordan beregne buen for en baldakin hvis vi kjenner bøyeradius og buesektor?

Formelen vil se ut som P=pi*r*n/180, hvor:
- P er lengden på buen (i vårt tilfelle lengden på et polykarbonatark eller et profilrør, som vil bli et element i rammen).
- pi er tallet "pi" (i beregninger som ikke krever ekstremt høy nøyaktighet, vanligvis tatt lik 3,14).
- r er radiusen til buen.
- n er buevinkelen i grader.
La oss, som et eksempel, beregne lengden på baldakinbuen med egne hender med en radius på 2 meter og en sektor på 35 grader.
P \u003d 3,14 * 2 * 35 / 180 \u003d 1,22 meter.
I arbeidsprosessen oppstår ofte den motsatte situasjonen: det er nødvendig å justere buens radius og sektor til en fast lengde på buen. Årsakene er klare: prisen på polykarbonat er høy nok til å minimere mengden avfall.
I dette tilfellet vil selvsagt produktet av sektoren og radien være lik P/pi*180.
La oss prøve å passe buen under et standard ark 6 meter langt. 6/3,14*180=343,9 (med avrunding). Videre - et enkelt utvalg av verdier med en kalkulator i hånden: for eksempel, for en buesektor på 180 grader, kan du ta radius lik 343,9 / 180 \u003d 1,91 meter; med en radius på 2 meter, vil sektoren være lik 343,9 / 2 \u003d 171,95 grader.
Beregning etter akkorder
Hvordan ser beregningen av utformingen av en polykarbonatbaldakin med bue ut hvis vi bare har informasjon om avstanden mellom kantene på buen og høyden?
I dette tilfellet brukes den såkalte Huygens-formelen. For å bruke det, la oss mentalt dele akkorden som forbinder endene av buen i to, hvoretter vi tegner en vinkelrett på akkorden i midten.
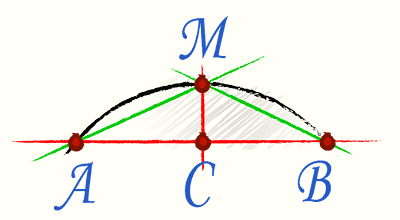
Selve formelen har formen Р=2l+1/3*(2l-L), der l er AM-akkorden og L er AB-akkorden.
Viktig: beregningen gir et omtrentlig resultat. Maksimal feil er 0,5 %; jo mindre vinkelsektor av buen, jo mindre feil.
La oss beregne lengden på buen for saken når AB \u003d 2 m og AM - 1,2 m.
P=2*1,2+1/3*(2*1,2-2)=2,4+1/3*0,4=2,533 meter.
Beregning av snittet med kjent bøyelast
Litt av en livssituasjon: en del av kalesjen er et visir av kjent lengde. Vi kan grovt anslå toppsnøbelastningen på den. Hvordan velge et profilrør av en slik seksjon for bjelker slik at det ikke bøyer seg under belastning?

Merk! Vi berører bevisst ikke hvordan vi skal beregne belastningen på kalesjen. Vurdering av snø- og vindbelastning er et helt selvforsynt tema for en egen artikkel.
For å regne ut trenger vi to formler:
- M = FL, der M er bøyemomentet, F er kraften som påføres enden av spaken i kilogram (i vårt tilfelle, vekten av snøen på visiret), og L er lengden på spaken (lengden av bjelken som bærer belastningen fra snøen, fra kant til spissfester) i centimeter.
- M/W=R, der W er motstandsmomentet og R er styrken til materialet.
Og hvordan vil denne haugen av ukjente verdier hjelpe oss?
I seg selv, ingenting. Noen referansedata mangler for beregningen.
| stålkvalitet | Styrke (R), kgf/cm2 |
| St3 | 2100 |
| St4 | 2100 |
| St5 | 2300 |
| 14G2 | 2900 |
| 15GS | 2900 |
| 10G2S | 2900 |
| 10G2SD | 2900 |
| 15HSND | 2900 |
| 10HSND | 3400 |
Referanse: St3, St4 og St5 stål brukes vanligvis til profesjonelle rør.
Nå, basert på dataene vi har, kan vi beregne bøyemotstandsmomentet til profilrøret. La oss gjøre det.
Anta at det samler seg 400 kilo snø på en to meter lang kalesje med tre bærebjelker laget av St3 stål.For å forenkle beregningene vil vi bli enige om at hele lasten faller på kanten av visiret. Åpenbart vil belastningen på hver bjelke være 400/3=133,3 kg; med en to-meters spak vil bøyemomentet være lik 133,3 * 200 \u003d 26660 kgf * cm.
Nå beregner vi motstandsmomentet W. Fra ligningen 26660 kgf * cm / W = 2100 kgf / cm2 (stålstyrke) følger det at motstandsmomentet skal være minst 26660 kgf * cm / 2100 kgf / cm2 = 12,7 cm3.
Hvordan vil verdien av motstandsmomentet føre oss til dimensjonene til røret? Gjennom sortimentstabellene i GOST 8639-82 og GOST 8645-68 regulerer dimensjonene til firkantede og formede rør. For hver størrelse indikerer de det tilsvarende motstandsmomentet, og for en rektangulær seksjon - langs hver av aksene.
Etter å ha sjekket tabellene finner vi ut at minimumsstørrelsen på et firkantet rør med de nødvendige egenskapene er 50x50x7,0 mm; rektangulær (med vertikal orientering av den større siden) - 70x30x5,0 mm.

Konklusjon
Vi håper at vi ikke har overarbeidet leseren med en overflod av tørre figurer og formler. Som alltid kan tilleggsinformasjon om metodene for beregning og utforming av polykarbonat baldakiner finnes i videoen i denne artikkelen. Lykke til!
Har artikkelen hjulpet deg?